浮点数的精度问题
一：浮点数储存结构
任何数据在内存中都是以二进制的形式存储的，浮点数也不例外，浮点数分为单精度与双精度
单精度浮点数float占4字节、32位
双精度浮点数double占8字节、64位。
遵循IEEE二进制算数标准；float和double的二进制存储结构都分成三部分：：符号位+指数位+尾数位。
| Sign/符号位 | Exponent/指数位 | Fraction/尾数位 | |
|---|---|---|---|
| 单精度 | 1 [31] | 8 [30-23] | 23 [22-00] |
| 双精度 | 1 [63] | 11 [62-52] | 52 [51-00] |
*单精度浮点数float***
第一位符号位，表示该数的正负，0表示正数，1表示负数
接下来8位表示该浮点数的指数位
最后的23位表示尾数部分
****双精度浮点数double*****
第一位符号位，表示该数的正负，0表示正数，1表示负数
接下来11位表示该浮点数的指数位
最后的52位表示尾数部分
二：十进制浮点数存储分析
2.1 思路
十进制浮点数若想保存到计算机内存中，必须首先转换成二进制浮点数，而为了区分精度，按照IEEE标准需要从二进制浮点数中提取三个部分：尾数位、指数位、符号位，这三部分才是计算机内存真正存储的二进制。
以单精度为例整体流程如下
我们就以十进制浮点数173.8125存成单精度float32位例展开介绍
2.2 十进制浮点数转成二进制、科学计数法
十进制浮点数转成二进制方法
⑴整数部分：
1、除以2，取出余数，商继续除以2，直到得到0为止，将取出的余数逆序
⑵小数部分：
1、乘以2，然后取出整数部分，将剩下的小数部分继续乘以2，然后再取整数部分，一直取到小数部分为零为止。
2、如果永远不为零，则按要求保留足够位数的小数，最后一位做0舍1入。将取出的整数顺序排列。示例：25. 625
⑴ 整数部分25：除以2，商继续除以2，直到商0为止，然后将余数逆序排列。
25 / 2 商12 余 1
12 / 2 商6 余 0
6 / 2 商3 余 0
3 / 2 商1 余 1
1 / 2 商0停止 余 1
得到余数结果逆序排序得到22的二进制是: 11001
⑵ 小数部分0.625：乘以2，取整，小数部分继续乘以2，取整，得到小数部分0为止，将整数结果顺序排列。
0.625*2 = 1.25 取整1 小数部分是0.25
0.25*2 = 0.5 取整0 小数部分是0.5
0.5*2 = 1.0 取整1 小数部分是0停止
得到整数结果顺序排序得到0.625的二进制是: 101
⑶ 最终结果：十进制：25.625 ！！！等于！！！二进制： 11001.101 二进制需要用科学计数法表示
二进制： 11001.101
科学计数法： 11001.101 = 1.1001101*2（4）
ps：科学计数法中1.1001101称之为浮点数的精度2.3 提取尾数位
以科学计数法1.1001101*2（4）为准，尾数位指的是小数点后的二进制，即1.1001101代表的尾数是0.1001101，为什么舍弃了小数点左侧的1？？？
因为十进制浮点数换算成二进制然后转化成科学计数法后小数点前面的一位一定是1（IEEE 标准要求浮点数必须是规范的。这意味着尾数的小数点左侧必须为 1，因此我们在保存尾数的时候，可以省略小数点前面这个 1，从而腾出一个二进制位来保存更多的尾数），因此可以不需要存储。
最后针对单精度23位的规定，如果小数点后的二进制位数不够23位，则补0，所以最终得到浮点数的尾数为
1001 1010 0000 0000 0000 0002.4 提取指数位
以科学计数法1.1001101*2（4）为准，指数位是在指数4的基础上通过移位存储原理得到的
移位存储原理如下
由于float32的指数位为8位，所以如果所有位都为0的话，可以表示0，所有位都为1的话，可以表示255，因此指数位的8位0000 0000~1111 1111与0~255的数值一一对应，可以进行表示。
但是！指数也分正负，所以正负各占一半，即指数的范围现在变为-127~128。
因此现在也需要二进制0000 0000~ 1111 1111与-127~128一一对应（注意：此处的二进制数只是与-127~128区间的数字有对应关系），如下图：
所以本身表示0的二进制0000 0000现在需要表示-127，本身表示255的二进制1111 1111现在需要表示128，这就造成了二进制本身表示的数值比现在需要表示的数值大了127（ps：也就是说此处的进制是机器数，而不是我们人的数字，机器数与人的数字之间存在着对应关系而已，机器数的价值在于符合计算机的物理运算原理，有了它才能够让计算机以自己简单的方式去运算人类数学层面的复杂运算），所以要想获得现在指数的二进制表示，需要将指数加127然后转换成二进制
浮点数25.625的指数位 4 + 127 = 131 然后将131转化成二进制 10000011（这就是浮点数在底层存储的8位指数位）
2.5 提取符号位
25.625是正数，所以符号位为0。
至此我们得到浮点数25.625的三部分
符号位：0
指数位：10000011
尾数位：1001 1010 0000 0000 0000 000合在一起浮点数25.625在计算机底层存储的结构为： 0 10000011 10011010000000000000000
2.6 练习以单精度存储浮点数0.15625
十进制浮点数0.15625转成二进制的形式0.00101，过程略
二进制形式0.00101的科学计数法为：
依据科学计数法得到
尾数：1.01-1 得 .01，所以尾数位是：01000000000000000000000
指数：-3，移位存储 -3 + 127 得124，所以指数位是：1111100
符号：正数，所以符号位：0于是具体的存放方案如下
2.7 思考以单精度存储浮点数0.1的问题
0.1无法精确存储，因为十进制的0.1转换成二进制永远无法得到一个明确的结果
三：浮点运算的精度问题
十进制浮点数转成二进制然后得到的科学计数法所包含数字的个数称之为精度
比如我们上面得到的1.1001101相当于：精度为8
不是所有的浮点运算都有精度问题，而浮点数存在的精度问题主要来自于两个方面
1、首先十进制的浮点数转换成二进制的就不总是精确的，而只能是近似值，例如十进制的浮点数0.1
2、然后，即便十进制的浮点数转换成的二进制数是精确的，那么在存成单精度32bits或双精度64bits的过程中，同样可能会因为超出了23bits与52bits的限制而溢出，同样可能会出现不精确 了解
IEEE定义了多种浮点格式，但最常见的是三种类型：单精度、双精度、扩展双精度，分别适用于不同的计算要求。一般而言，单精度适合一般计算，双精度适合科学计算，扩展双精度适合高精度计算。一个遵循IEEE 754标准的系统必须支持单精度类型（强制类型）、最好也支持双精度类型（推荐类型），至于扩展双精度类型可以随意。单精度（Single Precision）浮点数是32位（即4字节）的，双精度（Double Precision）浮点数是64位（即8字节）的。
Go 平台上的浮点数类型 float 和 double 采纳了 IEEE 754 标准中所定义的单精度 32 位浮点数和双精度 64 位浮点数的格式，对应的类型分别是float32与float64。
根据IEEE（美国电气和电子工程师学会）754标准要求，无法精确保存的值必须向最接近的可保存的值进行舍入。这有点像我们熟悉的十进制的四舍五入，即不足一半则舍，一半以上（包括一半）则进。不过对于二进制浮 点数而言，还多一条规矩，就是当需要舍入的值刚好是一半时，不是简单地进，而是在前后两个等距接近的可保存的值中，取其中最后一位有效数字为零者。从上面 的示例中可以看出，奇数都被舍入为偶数，且有舍有进。我们可以将这种舍入误差理解为"半位"的误差。所以，为了避免 7.22 位对很多人造成的困惑，有些文章经常以 7.5 位来说明单精度浮点数的精度问题。
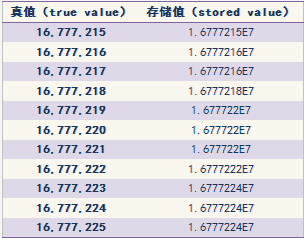
提示: 这里采用的浮点数舍入规则有时被称为舍入到偶数（Round to Even）。相比简单地逢一半则进的舍入规则，舍入到偶数有助于从某些角度减小计算中产生的舍入误差累积问题。因此为 IEEE 标准所采用。 对于单精度数，由于我们只有24位的尾数（其中一位隐藏,即1+23)，所以可以表达的最大指数为2^24 – 1 = 16,777,215。特别的，16,777,216 是偶数，所以我们可以通过将它除以 2 并相应地调整指数来保存这个数，这样16,777,216 同样可以被精确的保存。相反，数值16,777,217 则无法被精确的保存。由此，我们可以看到单精度的浮点数可以表达的十进制数值中，真正有效的数字不高于 8 位。
事实上，对相对误差的数值分析结果显示有效的精度大约为 7.22 位。
所以在go中关于下述浮点运算的误差，你便可以理解了
例1：因为溢出而导致精度问题
var f float32 = 16777216 // 1 << 24
fmt.Println(f == f+1) // "true"!，因为f+1的结果溢出了，所以f+1得到的还是16777216 例2：因为近似值而导致精度问题
var x=0.1 // 十进值的浮点数在转成二进制时拿到的就是一个近似值，存变量x的时候就出现了精度问题
var y=0.2
var z= x+y // 取出变量x在内存中的非精确值进行运算，必然结果有精度问题
fmt.Println(z) // 0.30000000000000004
fmt.Println(z == 0.3) // "false"!
// 注意：此处拿到的不是上面那个不精确的x，而是一个实实在在的0.1，所以结果为true
fmt.Println(0.1+0.2==0.3) // true 解决精度问题，用decimal，底层对浮点数的处理用的是字符串
package main
import (
"fmt"
"github.com/shopspring/decimal"
)
func main() {
// =================精度问题==================
//var a float64=1.5
//var b float64=1.3
//var result float64=a-b
//
//fmt.Printf("%.20f\n ",result) // 0.19999999999999995559
//fmt.Println(result == 0.2) // false
//
//
//var c float64 = 78.6
//fmt.Println(int64(c *100)) //浮点数运算后，转换成int64位
// =================解决方案==================
num1:=decimal.NewFromFloat(1.5)
num2:=decimal.NewFromFloat(1.2)
num3:=decimal.NewFromFloat(0.3)
//
res1:=num1.Sub(num2)
fmt.Println(res1.Cmp(num3)) // 返回0代表成立
//
num4:=decimal.NewFromFloat(78.6)
num5:=decimal.NewFromFloat(100)
res2:=num4.Mul(num5) //num4*num5
fmt.Println("结果是:",res2.String())
} ps：字符串也可以转成decimal,
package main
import (
"log"
"github.com/shopspring/decimal"
)
func main() {
xdecimal, err := decimal.NewFromString("1129.6")
if err != nil {
log.Println("转化decimal失败", err)
}
ydecimal := decimal.NewFromFloat(3)
resultdecimal := xdecimal.Mul(ydecimal)
log.Println(resultdecimal) //112960
}
如果对精度的要求只是保留到小数点后几位，我们也可以自定义函数来实现
package main
import (
"fmt"
"strconv"
)
// 截取小数位数
func Decimal(f float64, n int) float64 {
// strconv.Itoa()函数的参数是一个整型数字，它可以将数字转换成对应的字符串类型的数字
format := "%." + strconv.Itoa(n) + "f"
res, _ := strconv.ParseFloat(fmt.Sprintf(format, f), 64)
return res
}
func main() {
var x = 0.1
var y = 0.2
var z = x + y
fmt.Println(z == 0.3) // false
fmt.Println(0.1+0.2 == 0.3) // true
z = Decimal(z, 1)
fmt.Println(z == 0.3) // true
}扩展阅读：
https://blog.csdn.net/u010379324/article/details/90581631#_136