集成学习基础
集成学习(ensemnle learning)通过构建并结合多个学习器来完成学习任务,集成学习可以用于分类问题集成、回归问题集成、特征选取集成、异常点检测集成等等。
集成学习基础学习目标
- 集成学习构成
- Boosting和Bagging
- 平均法、投票法和学习法
集成学习基础引入
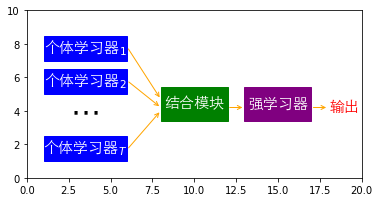
如上图所示,集成学习可以理解成,若干个个体学习器,通过结合策略构造一个结合模块,形成一个强学习器。其中所有的个体学习器中,可以是相同类型也可以是不同类型的个体学习器。
因此为了获得强学习器,我们首先得获得若干个个体学习器,之后选择一种较好的结合策略。
集成学习基础详解
个体学习器
上一节我们讲到,构造强学习器的所有个体学习器中,个体学习器可以是相同类型的也可以是不同类型的,对于相同类型的个体学习器,这样的集成是同质(homogeneous)的,例如决策树集成中全是决策树,神经网络集成中全是神经网络;对于不同类型的个体学习器,这样的集成是异质(heterogenous)的,例如某个集成中既含有决策树,又含有神经网络。
目前最流行的是同质集成,在同质集成中,使用最多的模型是CAR$T$决策树和神经网络,并且个体学习器在同质集成中也被称为弱学习器(weak learner)。按照同质弱学习器之间是否存在依赖关系可以将同质集成分类两类:第一个是弱学习器之间存在强依赖关系,一系列弱学习器基本都需要串行生成,代表算法是Boosting系列算法;第二个是弱学习器之间没有较强的依赖关系,一系列弱学习器可以并行生成,代表算法是Bagging和随机森林(random forest)系列算法。
Boosting
Boosting是一种可将弱学习器提升为强学习器的算法。它的工作机制为:先从初始训练集中训练出一个弱学习器,再根据弱学习器的表现对训练样本分布进行调整,使得先前弱学习器训练错误的样本权重变高,即让错误样本在之后的弱学习器中受到更多关注,然后基于调整后的样本分布来训练下一个弱学习器。
不断重复上述过程,直到弱学习器数达到事先指定的数目$T$,最终通过集合策略整合这$T$个弱学习器,得到最终的强学习器。
Boosting系列算法中最著名的算法有AdaBoost算法和提升树(boosting tree)系列算法,提升树系列算法中应用最广泛的是梯度提升树(gradient boosting tree)。
Boosting由于每一个弱学习器都基于上一个弱学习器,因此它的偏差较小,即模型拟合能力较强,但是模型泛化能力会稍差,即方差偏大,而Boosgting则是需要选择一个能减小方差的学习器,一般选择较简单模型,如选择深度很浅的决策树。
Bagging
Boosting的弱学习器之间是有依赖关系的,而Bagging的弱学习器之间是没有依赖关系的,因此它的弱学习器是并行生成。
Bagging的弱学习器的训练集是通过随机采样得到的。通过$T$次的随机采样,我们可以通过自主采样法(bootstrap sampling)得到$T$个采样集,然后对于这$T$个采样集独立的训练出$T$个弱学习器,之后我们通过某种结合策略将这$T$个弱学习器构造成一个强学习器。
Bagging系列算法中最著名的算法有随机森林,但是随机森林可以说是一个进阶版的Bagging算法,虽然随机森林的弱学习器都是决策树,但是随机森林在Baggin的样本随机采样的基础上,又进行了特征的随机选择。
Bagging由于通过随机采样获得数据,因此它的方差较小,即模型泛化能力较强,但是模型拟合能力较弱,即偏差偏大,而Bagging则是需要选择一个能减小偏差的学习器,一般选择较复杂模型,如选择深度很深的决策树或不剪枝的决策树。
自助采样法
给定包含$m$个样本的数据集,我们先随机取出一个样本放入采样集中,再把该样本放回初始数据集,使得下次采样时该样本仍有可能被选中,这样经过$m$次随机采样操作,我们能得到包含$m$个样本的采样集。
结合策略
构造强学习器除了需要使用若干个弱学习器之外,还需要选择某种结合策略,接下来我们将讲平均法、投票法和学习法三种结合策略。
假设集成包含$T$个弱学习器${h_1,h_2,\cdots,h_T}$,其中$h_i$在实例$X$上的输出为$h_i(X)$。
平均法
平均法一般用于解决数值类的回归问题,即对$T$个弱学习器的输出求平均值作为最终的输出。
- 简单平均法(simple averaging)
$$
H(X) = {\frac{1}{T}}\sum_{i=1}^T h_i(X)
$$ - 加权平均法(weighted averaging)
$$
H(X) = \sum_{i=1}^T w_i h_i(X)
$$
其中$w_i$是弱学习器$h_i$的权重,通常有$wi\geq0,\sum{i=1}^Tw_i=1$
投票法
投票法一般用于解决分类问题,假设我们需要预测的类别为${c_1,c_2,\cdots,c_K}$,对于样本$X$上的输出表示为一个$K$维向量$(h_i^1(X);h_i^2(X);\cdots;h_i^K(X))$,其中$h_i^j(X)$是$h_i$在类别标记$c_j$上的输出。
- 绝对多数投票法(majority voting)
$$
H(X) =
\begin{cases}
cj, \quad if\,\sum{i=1}^Thi^j(X)>{\frac{1}{2}}\sum{k=1}^K\sum_{i=1}^Th_i^k(X) \
不预测, \quad\text{其他情况}
\end{cases}
$$
绝对多数投票法即表示为:如果某标记得票数超过总票数一半的数量,则预测为该标记;否则不进行预测。 - 相对多数投票法(plurality voting)
$$
H(X) = c_{\underbrace{arg\,max}j\sum{i=1}^Th_i^j(X)}
$$
相对多数投票法即表示为:预测为得票数最多的标记,如果同时有多个标记获得最高票,则随机选择一个标记。 - 加权投票法(weighted voting)
$$
H(X) = c_{\underbrace{arg\,max}j\sum{i=1}^Tw_ih_i^j(X)}
$$
加权投票法和加权平均法类似,$w_i$是$h_i$的权重,通常有$wi\geq0,\sum{i=1}^Tw_i=1$
学习法
平均法和投票法相比较学习法都很简单,并且他们的误差较大,而学习法相比较则误差较小。
学习法中的代表方法是Stacking,当使用Stacking的结合策略时,我们不再是对弱学习器的结果做简单的处理,而是再加上一层学习器,与此同时,我们把个体学习器称为初级学习器,额外加上的学习器称为次级学习器或元学习器(meta-learner)。
Stacking结合策略可以这样理解:对于训练集,我们将初级学习器对训练集的学习结果作为次级学习器的输入,将训练集的标记仍当做样例标记,重新训练一个次级学习器得到最终结果;对于测试集,我们首先用初级学习器预测一次,得到次级学习器的输入样本,再用次级学习器预测一次,得到最终的预测结果。
小结
集成学习可以简单的认为通过某种结合策略将多个弱学习器构造成一个强学习器,奥卡姆剃刀原则——简单其实就是最好的。那为什么要花这么大的功夫把弱学习器结合成强学习器呢?至于构造的强学习器能有什么优点,接下来将会逐一介绍。