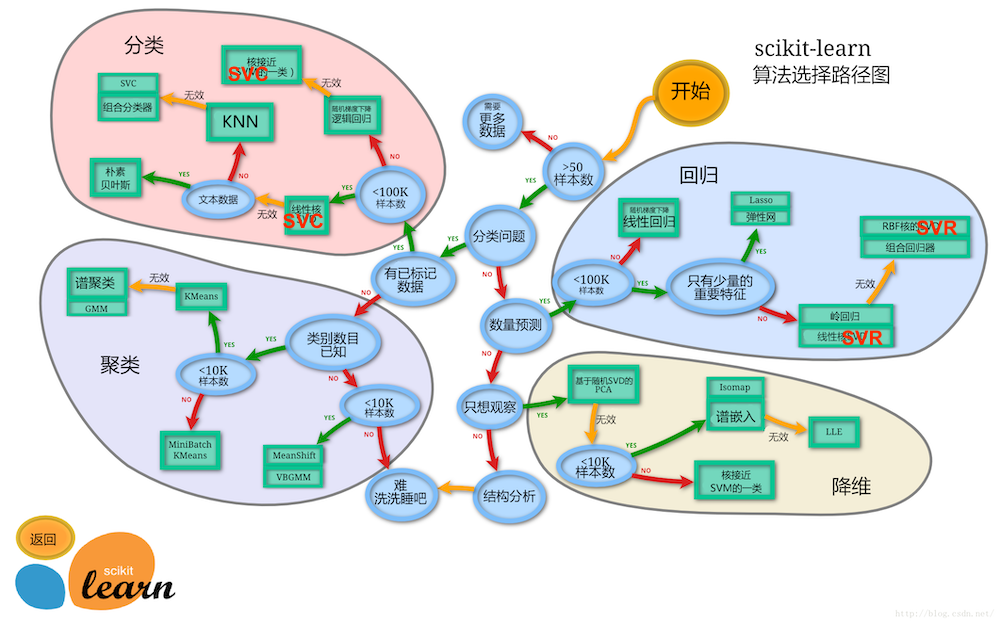
细分构建机器学习应用程序的流程-模型优化

  通过数据收集、数据预处理、训练模型、测试模型上述四个步骤，一般可以得到一个不错的模型，但是一般得到的都是一个参数收敛的模型，然而我们模型还有超参数或不同的核函数等，如r的非线性支持向量机的bf核或linear核；rbf核的非线性支持向量机超参数$C、\gamma$，正则化中的$\alpha$。我们模型优化一块主要是对模型超参数的优化，简而言之就是输入一组超参数，对每个超参数对应的模型进行测试，选择这一组超参数中最优的模型。

1.1 网格搜索法

  网格搜索法相当于对你输入的每一个参数都进行验证，并且可以设置多个超参数。

from sklearn import datasets
from sklearn.svm import SVC
from sklearn.model_selection import ShuffleSplit
from sklearn.model_selection import GridSearchCV
 
iris = datasets.load_iris()
X = iris.data
y = iris.target
 
# 总共有2*4=8种选择
parameters = {'kernel': ('linear', 'rbf'), 'C': [0.1, 1, 10, 100]}
 
svc = SVC(gamma="scale")
 
cv = ShuffleSplit(n_splits=10, test_size=0.3, random_state=1)
 
scoring = 'accuracy'
 
clf = GridSearchCV(svc, parameters, cv=cv, scoring=scoring)
clf.fit(X, y)

				

					
				
				

					
				
				

					
				
				

					
				
			

GridSearchCV(cv=ShuffleSplit(n_splits=10, random_state=1, test_size=0.3, train_size=None),
       error_score='raise-deprecating',
       estimator=SVC(C=1.0, cache_size=200, class_weight=None, coef0=0.0,
  decision_function_shape='ovr', degree=3, gamma='scale', kernel='rbf',
  max_iter=-1, probability=False, random_state=None, shrinking=True,
  tol=0.001, verbose=False),
       fit_params=None, iid='warn', n_jobs=None,
       param_grid={'kernel': ('linear', 'rbf'), 'C': [0.1, 1, 10, 100]},
       pre_dispatch='2*n_jobs', refit=True, return_train_score='warn',
       scoring='accuracy', verbose=0)