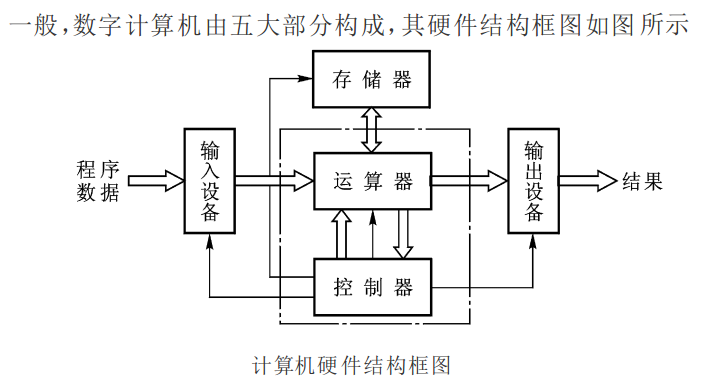
一、"体育竞技分析"问题分析
1.1 问题分析
体育竞技分析

高手过招,胜负只在毫厘之间
- 需求:毫厘是多少?如何科学分析体育竞技比赛?
- 输入:球员的水平
- 输出:可预测的比赛成绩
1.2 体育竞技分析:模拟N场比赛
- 计算思维:抽象 + 自动化
- 模拟:抽象比赛过程 + 自动化执行N场比赛
- 当N越大时,比赛结果分析会越科学
1.3 比赛规则
- 双人击球比赛:A & B,回合制,5局3胜
- 开始时一方先发球,直至判分,接下来胜者发球
- 球员只能在发球局得分,15分胜一局
二、自顶向下和自底向上
2.1 自顶向下(设计)
解决复杂问题的有效方法
- 将一个总问题表达为若干个小问题组成的形式
- 使用同样方法进一步分解小问题
- 直至,小问题可以用计算机简单明了的解决

2.2 自底向上(执行)
逐步组建复杂系统的有效测试方法
- 分单元测试,逐步组装
- 按照自顶向下相反的路径操作
- 直至,系统各部分以组装的思路都经过测试和验证

三、"体育竞技分析"实例讲解
3.1 体育竞技分析
程序总体框架及步骤
- 步骤1:打印程序的介绍性信息
- 步骤2:获得程序运行参数:proA, proB, n
- 步骤3:利用球员A和B的能力值,模拟n局比赛
- 步骤4:输出球员A和B获胜比赛的场次及概率
- printInfo()
- getInputs()
- simNGames()
- printSummary()
3.2 第一阶段:程序总体框架及步骤

def main():
printIntro()
probA, probB, n = getInputs()
winsA, winsB = simNGames(n, probA, probB)
printSummary(winsA, winsB)
def printIntro():
"""介绍性内容,提高用户体验"""
print("这个程序模拟两个选手A和B的某种竞技比赛")
print("程序运行需要A和B的能力值(以0到1之间的小数表示)")
def getInputs():
a = eval(input("请输入选手A的能力值(0-1): "))
b = eval(input("请输入选手B的能力值(0-1): "))
n = eval(input("模拟比赛的场次: "))
return a, b, n
def printSummary(winsA, winsB):
n = winsA + winsB
print("竞技分析开始,共模拟{}场比赛".format(n))
print("选手A获胜{}场比赛,占比{:0.1%}".format(winsA, winsA/n))
print("选手B获胜{}场比赛,占比{:0.1%}".format(winsB, winsB/n))3.3 第二阶段:步骤3 模拟N局比赛

def simNGames(n, probA, probB):
winsA, winsB = 0, 0
for i in range(n):
scoreA, scoreB = simOneGame(probA, probB)
if scoreA > scoreB:
winsA += 1
else:
winsB += 1
return winsA, winsB3.4 第三阶段
根据分数判断局的结束

def simOneGame(probA, probB):
scoreA, scoreB = 0, 0
serving = "A"
while not gameOver(scoreA, scoreB):
if serving == "A":
if random() < probA:
scoreA += 1
else:
serving = "B"
else:
if random() < probB:
scoreB += 1
else:
serving = "A"
return scoreA, scoreB
def gameOver(a,b):
return a==15 or b==15
四、"体育竞技分析"举一反三
4.1 理解自顶向下和自底向上
- 理解自顶向下的设计思维:分而治之
- 理解自底向上的执行思维:模块化集成
- 自顶向下是“系统”思维的简化
4.2 应用问题的扩展
- 扩展比赛参数,增加对更多能力对比情况的判断
- 扩展比赛设计,增加对真实比赛结果的预测
- 扩展分析逻辑,反向推理,用胜率推算能力?