非线性支持向量机
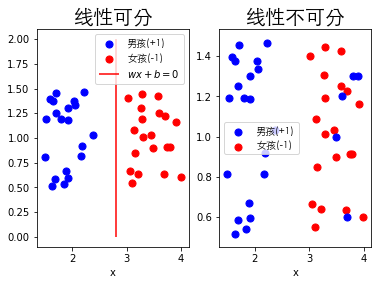
支持向量机分为三种,线性可分支持向量机和线性支持向量机都是对线性可分的数据做处理,线性支持向量机也仅仅是对异常值做处理,并不是真正的对非线性可分数据做处理,接下来将会介绍支持向量机的第三种方法非线性支持向量机(non-linear support vector machine)。
非线性支持向量机学习目标
- 核技巧
- 正定核函数
- 常用的4个核函数
- 非线性支持向量机的步骤
非线性支持向量机详解
多项式回归和非线性支持向量机
曾在线性回归中讲到过多项式回归,此处只做简单回顾。
假设一个正方体的房子的价格与房子的边长、房子的占地面积和房子的体积有关系,然而现在只有房子的边长$x_1$一个特征,如果只拿特征去预测房子的价格,则有很大可能会欠拟合,因此需要增加房子的占地面积和体积这两个特征,即
$$
\hat{y} = \omega_1x_1 + \omega_2{x_1}^2 + \omega_3{x_1}^3 + b
$$
令$x_1=x_1,x_2={x_1}^2,x_3={x_1}^3$,则多项式的线性模型变成
$$
\hat{y} = \omega_1x_1 + \omega_2x_2 + \omega_3x_3 + b
$$
通过上述转变可以看到把线性回归转换成多项式回归之后又变回了线性回归,即对于一维不是线性的数据,把它映射到了三维之后,数据则变成了线性的数据。
其实非线性支持向量机即运用了这个思想,即非线性支持向量机把低维特征数据映射到高维,让数据变得线性可分,此时问题就变成了线性可分的数据分类问题。
核技巧
核函数引入
首先回顾线性支持向量机的目标函数的优化问题为
$$
\begin{align}
& \underbrace{\min}{\alpha} {{\frac{1}{2}}\sum{i=1}^m\sum_{j=1}^m\alpha_i\alpha_jy_iy_j(x_ixj)-\sum{i=1}^m\alphai} \
& s.t. \quad \sum{i=1}^m\alpha_iy_i=0 \
& \quad\quad 0\leq\alpha_i\geq{C}
\end{align}
$$
从上式可以发现线性支持向量机的目标函数对于特征的处理是以$x_ixj$的形式出现的,此时如果定义一个低维特征空间到高维特征空间的映射函数$\phi(x)$,让所有特征映射到一个更高的维度,让数据线性可分,因此则可以继续按照线性支持向量机的方法优化目标函数,进而求出分离超平面和分类决策函数,即线性支持向量机的目标函数的优化问题变成了
$$
\begin{align}
& \underbrace{\min}{\alpha} {{\frac{1}{2}}\sum{i=1}^m\sum{j=1}^m\alpha_i\alpha_jy_iy_j(\phi(x_i)\phi(xj))-\sum{i=1}^m\alphai} \
& s.t. \quad \sum{i=1}^m\alpha_iy_i=0 \
& \quad\quad 0\leq\alpha_i\geq{C}
\end{align}
$$
可以发现使用该方法貌似完美的解决了该问题,并且由于只是改动了数据的特征维度,但是之前一直使用的数据都是测试数据,如果真的到了生产上,那么特征可能不仅仅就是1个、2个,而是成千上万个,如果再对特征进行映射处理,那么特征的维度的快速增加,计算强度也随之增加,而且遇到无穷维的特征,那么根本无法计算,所以这并不是很合理的。而核函数则很好的解决了计算量大的问题。
核函数
设$X$是低维输入空间(欧式空间$R^n$的子集或离散集合),$H$为高维特征空间(希尔伯特空间),若果存在一个从$X$到$H$的映射$\phi(x):X \rightarrow H$使得对所有的$x,z\in{X}$,函数$K(x,z)$满足条件
$$
K(x,z)=\phi(x)\phi(z)
$$
则称$K(x,z)$为核函数,$\phi(x)$为映射函数,式中的$\phi(x)\phi(z)$为$\phi(x)$和$\phi(z)$的内积。
由于$x,z\in{X}$,在计算$K(x,z)$的时候是在低维输入空间$R^n$中直接计算的,而不是通过$\phi(x)\phi(z)$计算出$K(x,z)$,因为$\phi$是输入空间$R^n$到特征空间$H$的映射,特征空间$H$一般是高维的,甚至是无穷维的,并且就算给定了核$K(x,z)$,特征空间和映射函数也不是唯一的,可以有多种不同的映射关系即不同的特征空间,即使是在同一特征空间里也可以取不同的映射关系。
总而言之核函数的好处在于它在低维空间上计算,而将实质上的分类效果即内及计算表现在了高维空间中,因此避免了直接在高维中的复杂计算。
通过使用核函数$K(x,z)$后非线性支持向量机的分离超平面为
$$
\sum{i=1}^m \sum{i=1}^m{\alpha_i}^y_iK(x,x_i)+b^ = 0
$$
分类决策函数为
$$
f(x) = sign(\sum_{i=1}^m{\alpha_i}^y_iK(x,x_i)+b^)
$$