细分构建机器学习应用程序的流程-训练模型
1.1 训练回归模型
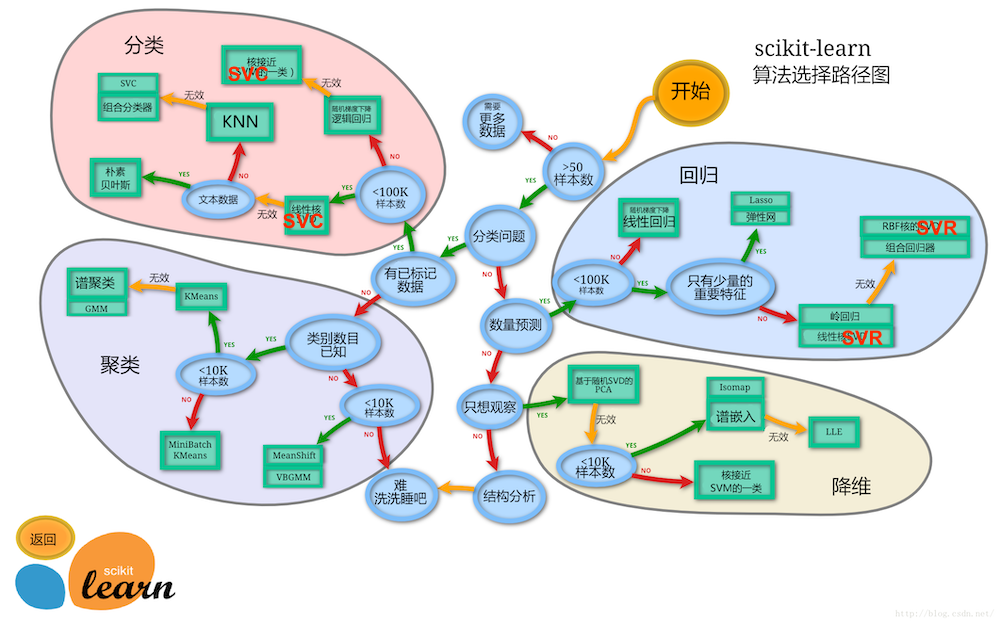
接下来我们将用波士顿房价数据集来介绍我们的回归模型,波士顿总共有506条数据,所以样本数小于100K,依据地图可以先使用Lasso回归-弹性网络回归-岭回归-线性支持向量回归-核支持向量回归-决策树回归-随机森林回归
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from matplotlib.font_manager import FontProperties
from sklearn import datasets
%matplotlib inline
font = FontProperties(fname='/Library/Fonts/Heiti.ttc')
# 设置numpy数组的元素的精度(位数)
np.set_printoptions(precision=4, suppress=True)boston = datasets.load_boston()
len(boston.target)506X = boston.data
X[:5]array([[ 0.0063, 18. , 2.31 , 0. , 0.538 , 6.575 ,
65.2 , 4.09 , 1. , 296. , 15.3 , 396.9 ,
4.98 ],
[ 0.0273, 0. , 7.07 , 0. , 0.469 , 6.421 ,
78.9 , 4.9671, 2. , 242. , 17.8 , 396.9 ,
9.14 ],
[ 0.0273, 0. , 7.07 , 0. , 0.469 , 7.185 ,
61.1 , 4.9671, 2. , 242. , 17.8 , 392.83 ,
4.03 ],
[ 0.0324, 0. , 2.18 , 0. , 0.458 , 6.998 ,
45.8 , 6.0622, 3. , 222. , 18.7 , 394.63 ,
2.94 ],
[ 0.0691, 0. , 2.18 , 0. , 0.458 , 7.147 ,
54.2 , 6.0622, 3. , 222. , 18.7 , 396.9 ,
5.33 ]])y = boston.target
yarray([24. , 21.6, 34.7, 33.4, 36.2, 28.7, 22.9, 27.1, 16.5, 18.9, 15. ,
18.9, 21.7, 20.4, 18.2, 19.9, 23.1, 17.5, 20.2, 18.2, 13.6, 19.6,
15.2, 14.5, 15.6, 13.9, 16.6, 14.8, 18.4, 21. , 12.7, 14.5, 13.2,
13.1, 13.5, 18.9, 20. , 21. , 24.7, 30.8, 34.9, 26.6, 25.3, 24.7,
21.2, 19.3, 20. , 16.6, 14.4, 19.4, 19.7, 20.5, 25. , 23.4, 18.9,
35.4, 24.7, 31.6, 23.3, 19.6, 18.7, 16. , 22.2, 25. , 33. , 23.5,
19.4, 22. , 17.4, 20.9, 24.2, 21.7, 22.8, 23.4, 24.1, 21.4, 20. ,
20.8, 21.2, 20.3, 28. , 23.9, 24.8, 22.9, 23.9, 26.6, 22.5, 22.2,
23.6, 28.7, 22.6, 22. , 22.9, 25. , 20.6, 28.4, 21.4, 38.7, 43.8,
33.2, 27.5, 26.5, 18.6, 19.3, 20.1, 19.5, 19.5, 20.4, 19.8, 19.4,
21.7, 22.8, 18.8, 18.7, 18.5, 18.3, 21.2, 19.2, 20.4, 19.3, 22. ,
20.3, 20.5, 17.3, 18.8, 21.4, 15.7, 16.2, 18. , 14.3, 19.2, 19.6,
23. , 18.4, 15.6, 18.1, 17.4, 17.1, 13.3, 17.8, 14. , 14.4, 13.4,
15.6, 11.8, 13.8, 15.6, 14.6, 17.8, 15.4, 21.5, 19.6, 15.3, 19.4,
17. , 15.6, 13.1, 41.3, 24.3, 23.3, 27. , 50. , 50. , 50. , 22.7,
25. , 50. , 23.8, 23.8, 22.3, 17.4, 19.1, 23.1, 23.6, 22.6, 29.4,
23.2, 24.6, 29.9, 37.2, 39.8, 36.2, 37.9, 32.5, 26.4, 29.6, 50. ,
32. , 29.8, 34.9, 37. , 30.5, 36.4, 31.1, 29.1, 50. , 33.3, 30.3,
34.6, 34.9, 32.9, 24.1, 42.3, 48.5, 50. , 22.6, 24.4, 22.5, 24.4,
20. , 21.7, 19.3, 22.4, 28.1, 23.7, 25. , 23.3, 28.7, 21.5, 23. ,
26.7, 21.7, 27.5, 30.1, 44.8, 50. , 37.6, 31.6, 46.7, 31.5, 24.3,
31.7, 41.7, 48.3, 29. , 24. , 25.1, 31.5, 23.7, 23.3, 22. , 20.1,
22.2, 23.7, 17.6, 18.5, 24.3, 20.5, 24.5, 26.2, 24.4, 24.8, 29.6,
42.8, 21.9, 20.9, 44. , 50. , 36. , 30.1, 33.8, 43.1, 48.8, 31. ,
36.5, 22.8, 30.7, 50. , 43.5, 20.7, 21.1, 25.2, 24.4, 35.2, 32.4,
32. , 33.2, 33.1, 29.1, 35.1, 45.4, 35.4, 46. , 50. , 32.2, 22. ,
20.1, 23.2, 22.3, 24.8, 28.5, 37.3, 27.9, 23.9, 21.7, 28.6, 27.1,
20.3, 22.5, 29. , 24.8, 22. , 26.4, 33.1, 36.1, 28.4, 33.4, 28.2,
22.8, 20.3, 16.1, 22.1, 19.4, 21.6, 23.8, 16.2, 17.8, 19.8, 23.1,
21. , 23.8, 23.1, 20.4, 18.5, 25. , 24.6, 23. , 22.2, 19.3, 22.6,
19.8, 17.1, 19.4, 22.2, 20.7, 21.1, 19.5, 18.5, 20.6, 19. , 18.7,
32.7, 16.5, 23.9, 31.2, 17.5, 17.2, 23.1, 24.5, 26.6, 22.9, 24.1,
18.6, 30.1, 18.2, 20.6, 17.8, 21.7, 22.7, 22.6, 25. , 19.9, 20.8,
16.8, 21.9, 27.5, 21.9, 23.1, 50. , 50. , 50. , 50. , 50. , 13.8,
13.8, 15. , 13.9, 13.3, 13.1, 10.2, 10.4, 10.9, 11.3, 12.3, 8.8,
7.2, 10.5, 7.4, 10.2, 11.5, 15.1, 23.2, 9.7, 13.8, 12.7, 13.1,
12.5, 8.5, 5. , 6.3, 5.6, 7.2, 12.1, 8.3, 8.5, 5. , 11.9,
27.9, 17.2, 27.5, 15. , 17.2, 17.9, 16.3, 7. , 7.2, 7.5, 10.4,
8.8, 8.4, 16.7, 14.2, 20.8, 13.4, 11.7, 8.3, 10.2, 10.9, 11. ,
9.5, 14.5, 14.1, 16.1, 14.3, 11.7, 13.4, 9.6, 8.7, 8.4, 12.8,
10.5, 17.1, 18.4, 15.4, 10.8, 11.8, 14.9, 12.6, 14.1, 13. , 13.4,
15.2, 16.1, 17.8, 14.9, 14.1, 12.7, 13.5, 14.9, 20. , 16.4, 17.7,
19.5, 20.2, 21.4, 19.9, 19. , 19.1, 19.1, 20.1, 19.9, 19.6, 23.2,
29.8, 13.8, 13.3, 16.7, 12. , 14.6, 21.4, 23. , 23.7, 25. , 21.8,
20.6, 21.2, 19.1, 20.6, 15.2, 7. , 8.1, 13.6, 20.1, 21.8, 24.5,
23.1, 19.7, 18.3, 21.2, 17.5, 16.8, 22.4, 20.6, 23.9, 22. , 11.9])from sklearn.model_selection import train_test_split
from sklearn.preprocessing import MinMaxScaler
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.3, random_state=1, shuffle=True)
print('训练集长度:{}'.format(len(y_train)), '测试集长度:{}'.format(len(y_test)))
scaler = MinMaxScaler()
scaler = scaler.fit(X_train)
X_train, X_test = scaler.transform(X_train), scaler.transform(X_test)
print('标准化后的训练数据:\n{}'.format(X_train[:5]))
print('标准化后的测试数据:\n{}'.format(X_test[:5]))训练集长度:354 测试集长度:152
标准化后的训练数据:
[[0.0085 0. 0.2815 0. 0.3148 0.4576 0.5936 0.3254 0.1304 0.229
0.8936 1. 0.1802]
[0.0022 0.25 0.1712 0. 0.1399 0.4608 0.9298 0.5173 0.3043 0.1851
0.7553 0.9525 0.3507]
[0.1335 0. 0.6466 0. 0.5885 0.6195 0.9872 0.0208 1. 0.9141
0.8085 1. 0.5384]
[0.0003 0.75 0.0913 0. 0.0885 0.5813 0.1681 0.3884 0.087 0.124
0.6064 0.9968 0.0715]
[0.0619 0. 0.6466 0. 0.6852 0. 0.8713 0.044 1. 0.9141
0.8085 0.8936 0.1487]]
标准化后的测试数据:
[[0.0006 0.33 0.063 0. 0.179 0.63 0.684 0.1867 0.2609 0.0668
0.617 1. 0.16 ]
[0.0003 0.55 0.1217 0. 0.2037 0.6007 0.5362 0.4185 0.1739 0.3492
0.5319 1. 0.1504]
[0.003 0. 0.2364 0. 0.1296 0.4731 0.8457 0.4146 0.087 0.0878
0.5638 0.9895 0.471 ]
[0.0007 0.125 0.2056 0. 0.0494 0.444 0.1638 0.4882 0.1304 0.3015
0.6702 0.9983 0.1758]
[0.0499 0. 0.6466 0. 0.7922 0.3451 0.9596 0.0886 1. 0.9141
0.8085 0.9594 0.2334]]1.1.1 Lasso回归
from sklearn.linear_model import Lasso
# Lasso回归相当于在普通线性回归中加上了L1正则化项
reg = Lasso()
reg = reg.fit(X_train, y_train)
y_pred = reg.predict(X_test)
print('所有样本误差率:\n{}'.format(np.abs(y_pred/y_test-1)))
'Lasso回归R2分数:{}'.format(reg.score(X_test, y_test))所有样本误差率:
[0.1634 0.0095 0.2647 0.0664 0.1048 0.0102 0.131 0.5394 0.0141 0.0309
0.0066 0.2222 0.1498 0.1839 0.1663 0.1924 0.4366 0.5148 0.0201 0.2684
0.3998 0.3775 0.0257 0.0433 0.032 1.374 0.5287 0.3086 0.4512 0.7844
0.0015 0.139 0.5067 0.7093 0.1734 0.0941 0.4246 0.3343 0.6761 0.1453
0.0459 0.1484 0.2167 0.4865 0.4501 1.391 0.5023 0.6975 0.0773 0.23
0.2403 0.0244 0.1593 0.0433 1.2819 0.071 1.9233 0.0837 0.254 0.4944
0.3093 0.1044 1.4394 0.4663 0.2188 0.3503 0.4062 0.4142 0.0567 0.0024
0.0396 0.7911 0.0091 0.0746 0.0823 0.0517 0.5071 0.0651 0.0139 0.3429
0.21 0.1955 0.3098 0.4897 0.0459 0.0748 0.6058 0.018 0.2064 0.1833
0.0054 0.517 0.556 0.0191 1.0166 0.1782 0.0312 0.0239 0.4559 0.0291
1.1285 0.3624 0.0518 0.0192 1.531 0.0605 0.8266 0.1089 0.2467 0.1109
0.4345 0.0151 0.8514 0.2863 0.3463 0.3223 0.2149 0.1205 0.2873 0.5277
0.1933 0.4103 0.0897 0.1084 0.0671 0.0542 0.023 0.1279 0.0502 0.139
0.1033 0.0069 0.0441 1.0007 0.0099 0.3426 0.4286 0.6492 0.4074 1.0538
0.1672 0.1838 0.0782 0.0069 0.1382 0.0446 0.0055 0.0687 0.1621 0.0338
0.316 0.4306]
'Lasso回归R2分数:0.21189040113362279'1.1.2 弹性网络回归
from sklearn.linear_model import ElasticNet
# 弹性网络回归相当于在普通线性回归中加上了加权的(L1正则化项+L2正则化项)
reg = ElasticNet()
reg = reg.fit(X_train, y_train)
y_pred = reg.predict(X_test)
'弹性网络回归R2分数:{}'.format(reg.score(X_test, y_test))'弹性网络回归R2分数:0.1414319491120538'1.1.3 岭回归
from sklearn.linear_model import Ridge
# 岭回归相当于在普通线性回归中加上了L2正则化项
reg = Ridge()
reg = reg.fit(X_train, y_train)
y_pred = reg.predict(X_test)
'岭回归R2分数:{}'.format(reg.score(X_test, y_test))'岭回归R2分数:0.7718570925003422'1.1.4 线性支持向量回归
from sklearn.svm import LinearSVR
# 线性支持向量回归使用的是硬间隔最大化,可以处理异常值导致的数据线性不可分
reg = LinearSVR(C=100, max_iter=10000)
reg = reg.fit(X_train, y_train)
y_pred = reg.predict(X_test)
'线性支持向量回归R2分数:{}'.format(reg.score(X_test, y_test))'线性支持向量回归R2分数:0.7825143888611817'