决策树CART算法
决策树C4.5算法虽然对决策树ID3算法做了很大的改良,但是缺点也是很明显的,无法处理回归问题、使用较为复杂的熵来作为特征选择的标准、生成的决策树是一颗较为复杂的多叉树结构,CART算法针对这些问题又做了进一步的优化。
决策树CART算法学习目标
- 基尼指数和熵
- CART算法对连续值和特征值的处理
- CART算法剪枝
- 决策树CART算法的步骤
- 决策树CART算法的优缺点
决策树CART算法详解
CART的英文名全称是classification and regression tree,所以有时候也把CART称它为分类回归树,分类回归树由特征选择、树的生成以及剪枝组成,既可以用于分类也可以用于回归。
基尼指数和熵
# 基尼指数和熵示例图
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.font_manager import FontProperties
%matplotlib inline
font = FontProperties(fname='/Library/Fonts/Heiti.ttc')
p = np.arange(0.001, 1, 0.001)
gini = 2*p*(1-p)
entropy = -(p*np.log2(p) + (1-p)*np.log2(1-p))/2
error = 1-np.max(np.vstack((p, 1-p)), 0)
plt.plot(p, entropy, 'r-', label='基尼指数')
plt.plot(p, gini, 'g-', label='熵之半$(1/2*H(p))$')
plt.plot(p, error, 'b-', label='分类误差率')
plt.xlabel('p', fontproperties=font)
plt.ylabel('损失', fontproperties=font)
plt.legend(prop=font)
plt.show()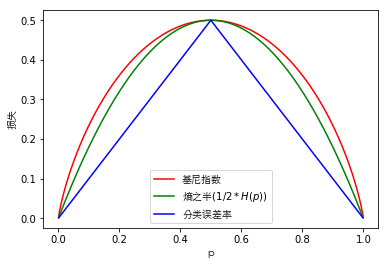
上图可以看出二分类问题中基尼指数和熵的曲线非常接近,因此基尼指数可以作为熵的一个近似替代。而CART算法就是使用了基尼指数来选择决策树的特征,同时为了进一步简化基尼指数的计算,CART算法每次对某个特征进行二分,因此CART算法构造的决策树是一颗二叉树模型。
CART算法对连续值特征的处理
CART算法类似于C4.5算法对连续值特征的处理,只是CART算法使用基尼指数取代了信息增益比对连续值做了处理。
假设现有一个特征$F$的特征值为连续值,从大到小排序为$f_1,f_2,\ldots,f_m$,CART算法对相邻样本间的特征值$fi,f{i+1}$取平均数,一共可以得到$m-1$个划分点,其中第$j$个划分点可以表示为
$$
S_j = {\frac {fi + f{i+1}} {2}}
$$
对于这$m-1$个划分点,分别计算以该点作为二元分类点的基尼指数,选择基尼指数最小的点作为该连续特征的二元离散分类点,把改点记作$f_t$,则特征值小于$f_t$的点记作$c_1$;特征值大于$f_t$的点记作$c_2$,这样就实现了连续特征值的离散化。
CART算法对离散值特征的处理
CART算法对离散值特征的处理采用的是不停的二分离散化特征的思想。
假设一个训练集$D$的某个特征$F$有$f_1,f_2,f_3$三种类别。如果我们使用的是ID3算法或者是C4.5算法,则会生成$3$个子节点,即三叉子节点,也因此导致决策树变成一颗多叉树。但是CART算法会基于这三个特征形成$f_1$和$f_2,f_3$、$f_2$和$f_1,f_3$、$f_3$和$f_1,f_2$这三种组合,并且在这三个组合中找到基尼指数最小的组合,然后生成二叉子节点。
假设$f_1$和$f_2,f_3$在这三者中基尼指数最小,则生成的二叉做子节点为$f_1$,二叉右子节点为$f_2,f_3$。由于右子节点并没有被完全分开,因此在之后会继续求出$f_2$和$f_3$的基尼指数,然后找到最小的基尼指数来划分特征$F$。
CART算法剪枝
回归CART树和分类CART树剪枝策略除了在特征选择的时候一个使用了均方误差,另一个使用了基尼指数,其他内容都一样。
无论是C4.5算法还是CART算法形成的决策树都很容易对训练集过拟合,因此可以使用剪枝的方式解决过拟合问题,这类似于线性回归中的正则化。
CART算法采用的事后剪枝法,即先生成决策树,然后产生所有可能的剪枝后的CART树,然后使用交叉验证来检验各种剪枝的效果,选择返回泛化能力最好的剪枝方法。即CART树的剪枝方法可分为两步:
- 使用原始的决策树$T_0$从它的底端开始不断剪枝,直到$T_0$的根节点生成一个子树序列${T_0,T_1,\ldots,T_n}$
- 通过交叉验证法选择泛化能力最好的剪枝后的树作为最终的CART树,即最优子树
生成剪枝后的决策树
在剪枝过程中,子树$T$的损失函数为
$$
C_\alpha(T) = C(T) + \alpha|T|
$$
其中$T$是任意子树,$\alpha \quad \alpha\geq0$为正则化参数,它权衡训练数据的拟合程度与模型的复杂度;$C(T)$是训练数据的预测误差(分类树使用基尼指数度量,回归树使用均方差度量),$|T|$是子树$T$的叶子节点的数量。
当$\alpha=0$时没有正则化,即原始的决策树为最优子树;当$\alpha$逐渐增大时,则正则化强度越大,生成的最优子树相比较原生的子树就越小;当$\alpha=\infty$时,即正则化强度达到最大,此时由原始的决策树的根节点组成的单节点树为最优子树。因此对于固定的$\alpha$,从子树的损失函数中可以看出一定存在使损失函数$C_\alpha(T)$最小的唯一子树$T_a$,$T_a$在损失函数最小的意义下是最优的。
可以递归的方法对书进行剪枝。将$\alpha$从小增大,$0=\alpha_0<\alpha_1<\cdots\alpha_n<+\infty$,产生一系列的区间$[\alphai,\alpha{i+1}),i=0,1,\ldots,n$;剪枝得到的子序列对应着区间$\alpha{\in}{[\alphai,\alpha{i+1})}$的最优子树序列${T_0,T_1,\ldots,T_n}$(注:每个区间内是有可能有多个子树的),序列中的子树是嵌套的。
从原始的决策树$T_0$开始剪枝,对$T0$的任意内部节点$t$,以$t$为单结点树的损失函数是
$$
C\alpha(t) = C(t) + \alpha
$$
以$t$为根节点的子树$Tt$的损失函数是
$$
C\alpha(T_t) = C(T_t) + \alpha|Tt|
$$
当$\alpha=0$以及$\alpha$充分小时(最优子树为原始的决策树),有不等式
$$
C\alpha(Tt) < C\alpha(t)
$$
当$\alpha$增大时,在某一$\alpha$有
$$
C_\alpha(Tt) = C\alpha(t)
$$
当$\alpha$继续增大时(最优子树为根节点组成的单节点树),有
$$
C_\alpha(Tt) > C\alpha(t)
$$
并且只要当$\alpha = {\frac {C(t)-C(T_t)} {|T_t|-1} }$(注:当$T_t$和$t$有相同的损失函数时该公式由$t$和$T_t$的损失函数联立得到)。由于$t$的节点少,因此$t$比$T_t$更可取,因此可以对子树$T_t$剪枝,也就是将它的子节点全部剪掉,变为一个叶子节点$t$。