常见的概率分布模型
离散概率分布函数
离散概率分布也称为概率质量函数(probability mass function),离散概率分布的例子有
伯努利分布(Bernoulli distribution)
二项分布(binomial distribution)
泊松分布(Poisson distribution)
几何分布(geometric distribution)等
连续概率分布函数
连续概率分布也称为概率密度函数(probability density function),它们是具有连续取值(例如一条实线上的值)的函数,连续概率分布的例子有
正态分布(normal distribution)
指数分布(exponential distribution)
β分布(beta distribution)等
联合分布函数
给定一个随机变量$(X,Y)$,称定义域为整个平面的二元实值函数
$$
F(x,y) = P(X\leq{x},Y\leq{y}) \quad -\infty\geq{x,y}\leq\infty
$$
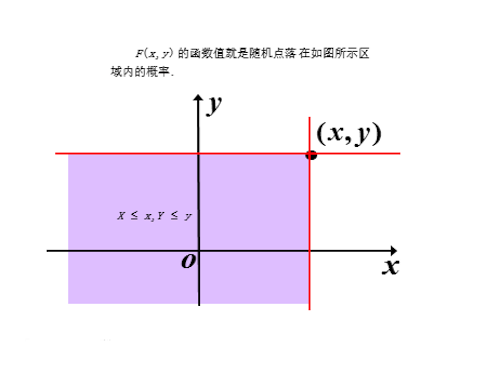
该二元实值函数为随机变量$(X,Y)$的分布函数,也可以称为是$(X,Y)$的联合分布函数。
按照联合分布函数的定义,$F(x,y)=P((X,Y)\in{D{xy}})$,其中$D{xy}$如下图所示
多项分布(Multinomial Distribution)
多项分布简介
多项分布是二项分布的推广,他们的区别是二项分布的结果只有$0$和$1$两种,多项式的结果可以有多个值。
多项分布的典型例子是掷骰子,6个点对应6个不同的数,每个点的概率都为${\frac{1}{6}}$
与二项分布类似,多项分布来自于$(p_1+p_2+\cdots+p_k)^n多项式的展开$
多项分布公式解析
以掷骰子为例,掷骰子的时候掷$1-6$的概率都为${\frac{1}{6}}$,记作$p_1-p_6$,可以发现$p_1+p_2+p_3+p_4+p_5+p_6=1$,现在把$p_1+p_2+p_3+p_4+p_5+p_6$记作做一次抽样各种事件发生的概率和,即可得$(p_1+p_2+p_3+p_4+p_5+p_6)^n=1^n$为$n$次抽样所有事件相互组合对应的概率和,之后使用多项式展开(注:使用多项式定理展开,由于多项式定理不在本节提及范围内,不多赘述),如果它不是掷骰子,而是一个有$n$种可能的问题,会得到一个多项式展开的公式
$$
P(X_1 = x_1,\ldots,X_k = x_k) = \begin{cases}
{\frac{n!}{x_1!\cdots{x_k!}}}(p^{x_1}\cdots{p^{xk})} \quad when\sum{i=1}^kx_i=n\
0 \quad otherwise \
\end{cases}
$$
这个多项式表示$X_1$出现$x_1$次,$X_2$出现$x_2$次,$\ldots$,$X_k$出现$x_k$次的出现概率,这样就得到了上述所示的多项分布的多项展开式公式。
伯努利分布(Bernoulli Distribution)
伯努利分布简介
伯努利分布是一个二值离散分布,结果只有$0$和$1$两种。
随即变量$X$为$1$的概率为$p$,则为$0$的概率为$q=1-p$,可以用公式表示为
$$
f(x) = p^x(1-p)^{1-x} = \begin{cases}
p, \quad\quad x=1 \
1-p, \quad x=0 \
\end{cases}
$$
伯努利分布的期望值和方差
伯努利分布的期望值为
$$
\begin{align}
E(X) & = \sum_{i=0}^1xif(x) \
& = 1p+0(1-p) \
& = p+0 \
& = p \
\end{align}
$$
伯努利分布的方差为
$$
\begin{align}
D(x) & = \sum{i=0}^1(x_i – E(x))^2f(x) \
& = (1-E(x))^2p + (0-E(x)^2(1-p) \
& = (1-p)^2p + (0-p)^2(1-p) \
& = p – p^2 \
& = p(1-p) \
& = pq
\end{align}
$$